4,000-ton trains around the curve, the grade throughout the length of the curve must be decreased. The amount to
reduce it is a problem of engineering beyond the scope of this text. Curves located on grades that have been
reduced in this way are said to be compensated.
3.5.
COMPUTING CURVATURE
The sharpness of a curve depends directly on the length
of its radius. Long radii result in light curvature; short radii, in
sharp.
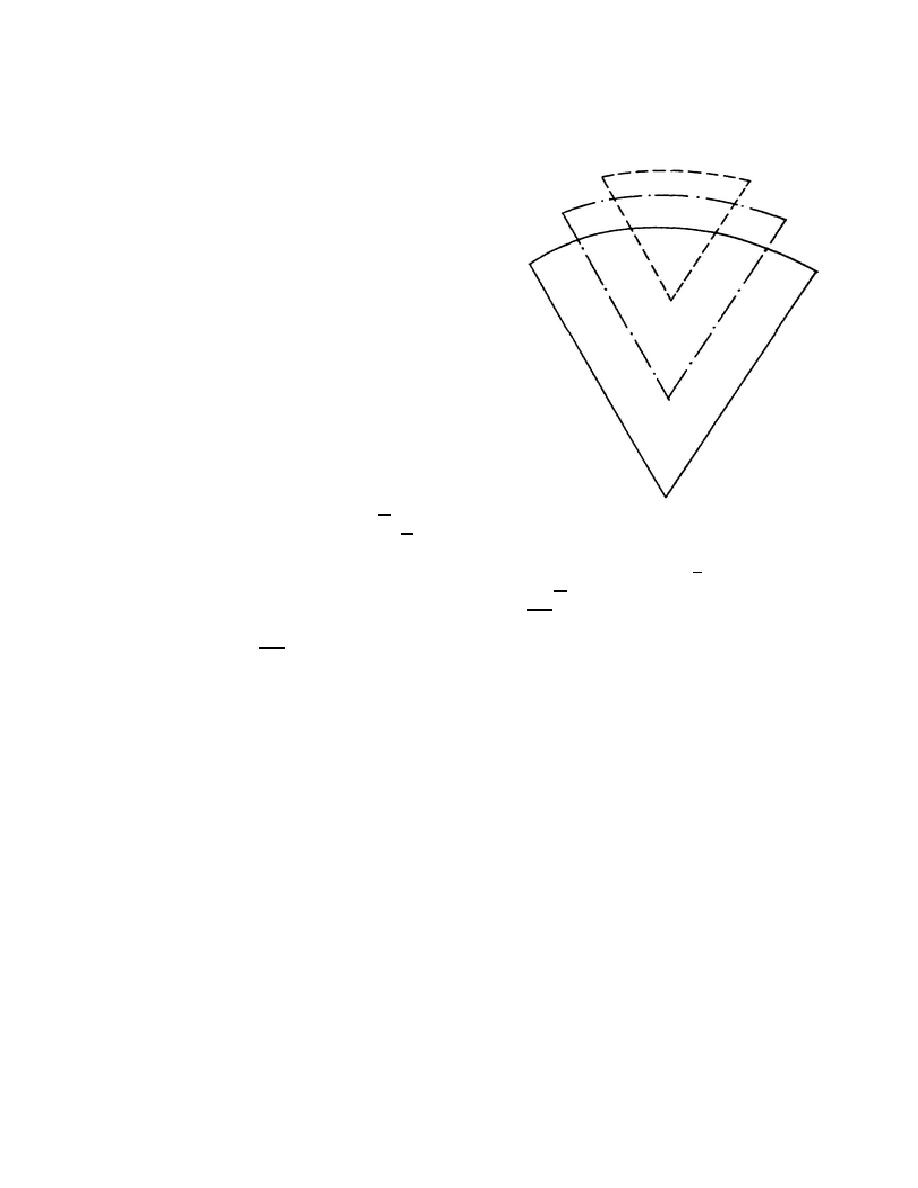
Compare the sharpness of the curves in the
accompanying sketch. Each of the three has the same number
of degrees; that is, each represents the same portion of an entire
circle. However, the curve with the short, broken line radii is
much sharper than the other two. At the same time, the curve
with the dot-dash radii is sharper than the one with the long,
solid-line radii. Most railroads, subways, and elevated lines in
countries other than the United States and Great Britain
designate the sharpness of a curve by specifying the radius. In
those two countries, it is given in degree of curvature.
The method of computing the degree of curvature of
track is shown in the two drawings in figure 3.2. A chord, 100
feet long, is placed so that the two ends touch the curved track,
on the inner side of the outside rail, at points A. A central angle
is formed by the two radii running to the center, C. The degree of curvature in the drawing at the left in figure 3.2
is 9 degrees, a much sharper curve than would be found on a main line. The degree of curvature in the drawing at
the right is 20 degrees, a much sharper curve than the 9-degree one. The dotted lines at d represent the same
portion of a circle as does the arc representing the track between points A. Since there are 360 degrees in a circle,
the 9-degree curvature illustrated represents 1/40th of a circle (360) and the 20-degree curvature illustrated
9
represents 1/18 of a circle (360).
20
64




 Previous Page
Previous Page
