moved or "thrown" at each station, expressed in eighths of an inch. If the throw is negative or minus, the track
must be moved in, that is, toward the low or inside rail. If the throw is positive or plus, the track must be moved
out, that is, toward the high or outside rail. When the full throws for all stations have been calculated, the
paperwork of stringlining is complete. Remember, there must never be any throw at the last station.
Sheet 2 of annex A is an overlay showing the same curve after the throws calculated in figure 3.5 have
been made. Place it over sheet 1, annex A, so that stations 0 and 9 coincide on the two sheets. You can then see
that the throwing results in a smooth curve, as intended.
3.23.
MARKED POINTS
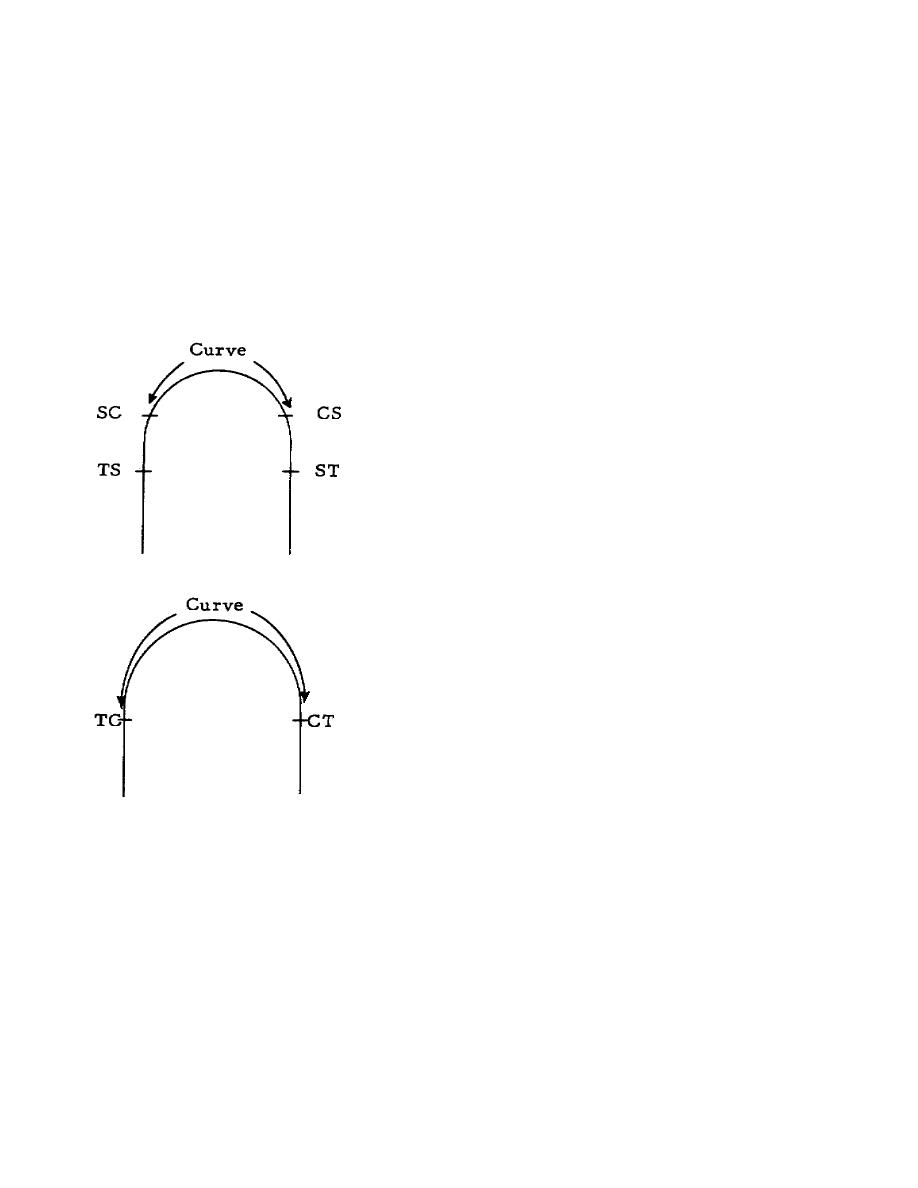
Many railway curves are marked with stakes to show where the tangents end, the spirals end, and so
forth. These points are shown in drawings, and may be marked in the field, by letters. As shown in the upper
sketch,
the
point where the tangent ends and the spiral begins is TS--tangent to spiral, while the point
where the
other spiral ends and the tangent begins is ST--spiral to tangent. The circular part of
a curve
begins at SC--spiral to curve, and ends at CS--curve to spiral. As shown in the
lower
sketch, if there are no spirals, the curve begins at TC--tangent to curve--and
ends at CT--curve to tangent.
When these points are marked by stakes, they help greatly in choosing proposed
ordinates. For example, the curvature between SC and CS is constant.
The correct proposed ordinate for this stretch is almost certainly the
average measured ordinate, to the nearest whole number, for the same distance.
When
ordinates have been assigned to the circular part of the curve, it is easy to set up
smooth spirals between TS and SC and between CS and ST. Remember,
though, that the sum of the proposed ordinates must always equal the sum of the
measured
ordinates. You can adjust your curve
81




 Previous Page
Previous Page
